My favorite is StalinSort. You go through the list and eliminate all elements which are not in line.
you should post this on lemmy.ml
it would be a pretty funny post for the full 5 minutes it would last until it got stalin sorted out of lemmy.ml
They would see nothing wrong with it
Do you not understand federation yet? https://lemmy.ml/post/22259107/14814668
this isn’t a community that they moderate tho
Moderators don’t have to come from the instance the community is hosted on necessarily.
No, but the point is that posting “Stalin executes people” jokes in .ml-run communities would not go over well.
I tend to prefer Hiroshima sort. Sorting completed in O(1) time, and it frees up memory too.
Underrated comment.
Reminds me of quantum-bogosort: randomize the list; check if it is sorted. If it is, you’re done; otherwise, destroy this universe.
Guaranteed to sort the list in nearly instantaneous time and with absolutely no downsides that are capable of objecting.
You still have to check that it’s sorted, which is O(n).
We’ll also assume that destroying the universe takes constant time.
In the universe where the list is sorted, it doesn’t actually matter how long the destruction takes!
It actually takes a few trillion years but its fine because we just stop considering the “failed” universes because they will be gone soon™ anyway.
Eh, trillion is a constant
We’ll also assume that destroying the universe takes constant time.
Well yeah just delete the pointer to it!
universe.take()
Except you missed a bug in the “check if it’s sorted” code and it ends up destroying every universe.
There’s a bug in it now, that’s why we’re still here.
deleted by creator
The creation and destruction of universes is left as an exercise to the reader
Creation is easy, assuming the many-worlds interpretation of quantum mechanics!
Instead of destroying the universe, can we destroy prior, failed shuffle/check iterations to retain o(1)? Then we wouldn’t have to reload all of creation into RAM.
Delete prior iterations of the loop in the same timeline? I’m not sure there’s anything in quantum mechanics to permit that…
What library are you using for that?
is-sorted and a handful of about 300 other npm packages. Cloning the repo and installing takes about 16 hours but after that you’re pretty much good for the rest of eternity
that explains why it took god 7 days to make the universe
We still suffer from the runtime errors that could’ve been caught at compilation time.
In Python you just use
import destroy_universe
Since randomizing the list increases entropy, it could theoretically make your cpu cooler just before it destroys the universe.
// portabilityGave me the giggles. I’ve helped maintain systems where this portable solution would have left everyone better off.
import yhwh def interventionSort(unsortedList): sortedList = yhwh.pray( "Oh great and merciful Lord above, let thine glory shine upon yonder list!", unsortedList ) return sortedListCamelcase in python, ew, a fundamentalist would do that
Where’s this yhwh library, can I install it with pip? Seems like it could have potential for some of my projects.
New templeOS fork?
yhwh looking suspiciously like an LLM
The most beautiful thing about this program is that it would work.
Various bit flips will once lead to all numbers being in the correct order. No guarantee the numbers will be the same, though…
Those bitflips are probably more likely to skip the section erroneously than waiting for the array to be sorted.
Fair enough! But won’t they flip again to start the program?
The OS would crash entirely before that happens
Reminds me of a program in Homestuck. It’s code that iterates until the author/universe dies, then executes some unknown code. The coding language is ~ath, or TilDeath.
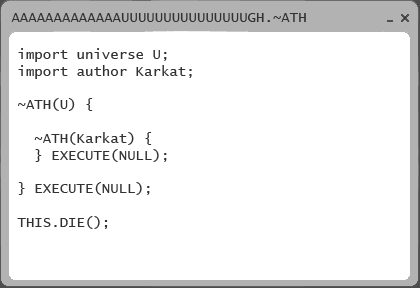
Might also take a very long time (or a large amount of radiation).
Not necessarily. I don’t have the numbers in front if me, but there is actually a probability that, past that point, something is so unlikely that you can consider it to be impossible (I.e. will never happen within the lifetime of the universe)
screw the universe we be flippin’ 😎🏄♀️
Yet… The chance is never zero 😁
I’m not sure there’s any guarantee that it will ever be sorted, since bit flips will be random and are just as likely to put it more out of order than more in order. Plus if there’s any error correction going on, it can cancel out bit flips entirely until up to a certain threshold.
Though I’m not sure if ECC (and other methods) write the corrected value back to memory or just correct the signals going to the core, so it’s possible they could still add up over time and overcome the second objection.
ECC (and other methods) write the corrected value back to memory
That was my understanding (it corrects the error and writes the good value back to RAM), but now I’m not so sure! I imagine it must do that, otherwise a second bit flip would actually corrupt the RAM, and the RAM manufacturer would want to reduce that risk.
Regular ECC adds an extra parity bit for each byte. For each byte of memory, it can correct an error in one bit, and detect but not correct an error in two bits, so they wouldn’t want a one bit error to linger for longer than it needs to.
CosmicRaySort.
I wonder how many 2 item lists have been sorted that way IRL.
you can also call it quantum sort since there is non zero probability that it will sort itself by random flips
It would actually have happened an infinite amount of times already, if either the universe is infinite, or there are infinite universes.
I really deeply hope the universe is finite for this reason. Every great or terrible thing always happens forever, there is no causality or consequence.
I prefer the one where you randomly sort the array until all elements are in order. ( Bogosort )
Bogosort is great! Also easy to implement
This is the algoritm I use at work.
Everyone does… it’s funny how it eventually works.
Shameless plug for my sort lib
edit: Looking at my old code it might be time to add typescript, es6 and promises to make it ✨ p r o d u c t i o n r e a d y ✨
Goos stuff, I will start using it. My code needs to chill out anyway
And the time complexity is only O(1)
I don’t think you can check if array of n elements is sorted in O(1), if you skip the check though and just assume it is sorted now (have faith), then the time would be constant, depending on how long you’re willing to wait until the miracle happens. As long as MTM (Mean Time to Miracle) is constant, the faithfull miracle sort has O(1) time complexity, even if MTM is infinite. Faithless miracle sort has at best the complexity of the algorithm that checks if the array is sorted.
Technically you can to down to O(0) if you assume all array are always sorted.
Oh yeah, I didn’t think about the time that it takes to check if it’s sorted. The sorting time is constant though
Hello programmers…
I recently took a course that went through basic python, C, and C++.
I had a hard time implementing various forms of sorting functions by hand (these were exercises for exam study). Are there any resources you folks would recommend so that I can build a better grasp of sorting implementations and efficiency?
don’t get discouraged. sorting algorithms occur frequently in interviews, and yes you use them a decent amount (especially in languages without built in sorts like c) but they are one of the harder things to visualize in terms of how they work. I’d say avoid anything recursive for now until you can get selection and insertion down pat. check out geeksforgeeks articles on them, but also don’t be afraid to Google willy nilly, you’ll find the resource that makes it click eventually.
in terms of efficiency, it does become a little more difficult to grasp without some math background. big o is known as asymptomatic notation, and describes how a function grows. for example, if you graph f1(x)=15log(x) and f2(x)=x, you’ll notice that if x is bigger than 19, then f2(x) always has a higher output value than f1(x). in computer science terms, we’d say f1 is O(log(n)), meaning it has logarithmic growth, and f2 is O(n), or linear growth. the formal definition of big o is that f(x) is O(g(x)), if and only if (sometimes abbreviated as iff) there exists constants N and C such that |f(x)| <= C|g(x)| for all x>N. in our example, we can say that C = 1, and N>19, so that fulfills definition as |15log(x)| <= 1|x| whenever x>19. therefore, f1(x) is O(f2(x)). apologies for just throwing numbers at you, (or if you’ve heard all this before) but having even just the most basic grasp of the math is gonna help a lot. again, in terms of best resources, geeksforgeeks is always great and googling can help you find thousands of more resources. trust that you are not the first person to have trouble with these and most people before you have asked online about it as well.
I also highly reccomend grabbing a copy of discrete mathematics and it’s applications by Kenneth Rosen to dig farther into the math. there’s a few other types of asymptomatic notation such os big omega and big theta, even little o, that I didn’t mention here but are useful for comparing functions in slightly different ways. it’s a big book but it starts at the bottom and is generally pretty well written and well laid out.
feel free to dm me if you have questions, I’m always down to talk math and comp sci.
edit: in our example, we could also pick c =19 and n = 1, or probably a few other combinations as well. as long as it fills the definition it’s correct.
Wait, that’s exactly how i tidy up my kitchen!
On a long enough time scale, yes, it will get tidy.













